QM metrology

Thermal effects in the 'real-world'

By Richard Clark

Anyone who’s experienced designing an in-house inspection lab or developed in-house calibration procedures to meet ISO-9000, QS-9000, or TS-16949 requirements has dealt with this (in)famous decree found in element 4.11.

"The supplier shall…ensure the environmental conditions are suitable for the calibrations, inspections, measurements, and tests being carried out."

If you cannot literally give a class on exactly what this does and does not mean, then you are at the mercy of your auditors, your customers, and the misperceptions that have been assumed true for quite some time. Unfortunately, for most who are tasked to set up an in-house measurement control system, the most accessible people to ask about thermal effects are our friends at the outside source calibration labs whom we depend on several times per year. These people are general extremely knowledgeable in this subject. The problem is they deal with these issues in situations where objects must be controlled and measured in increments as small as 5 millionths of an inch. These applications require ambient (air) temperature to remain around 68°F ±2° and gage temperatures around 68°F ±0.5°. Most industrial inspection facilities don’t measure parts in this "micro-world" but more in the "real-world."

To begin with, we should look at the very basic equation used to calculate thermal expansion.

Change in length = Original length x Coefficient of thermal expansion x Change in temperature from 20°C

Every man-made material on the face of the Earth has a coefficient of thermal expansion (CTE) and ASME Y14.5 – 1994 states "Unless otherwise specified, all dimensions are applicable at 20°C (68°F). Compensation may be made for measurements taken at other temperatures." If we wanted to calculate the thermal expansion of a 4" steel piece or gage block that was being measured in a 76°F environment we’d use the CTE for steel (0.0000115). 76°F represents a realistic shop temperature for 3 months out of the year.

Change in Length = 4.00000 x 0.0000115 x 4.44°C
Change in Length = 0.0002" (2 tenths)
Expanded Length = 4.0002"

Now we are right in the middle of no-man’s land. If we’re calibrating a caliper with an OEM accuracy tolerance of ±0.001", the caliper is not sensitive enough (with a resolution of 0.001") to detect the expansion of the gage block. The same concept would apply if we were measuring a 4" work piece which, because of an open tolerance, could be inspected with a caliper.

Fabulous!!! At 76°F we have not violated the mighty 4.11, but wait…what if we are inspecting a 4" work piece, using a 0.0001" resolution micrometer, and the tolerance of the piece is plus 0.0005" minus nothing? We measure the diameter 15 different times and get 4.0001" (12 times) and 4.0000" in 3 narrow places. Now our ace will surely get trumped. What consistently measures 4.0001" at 76°F is actually 3.9999" (0.0001" under specification) at 68°F. We should take notice at this time of the fact we’ve just discussed and "figured out" two very real thermal effect situations and we used nothing more than a $2 calculator.

Some people I’ve dealt with over the years insist "thermal effects aren’t real because parts expand and gages expand so it really doesn’t matter," or "Do we really have to recognize thermal effects?" (It’s a law of science. I suppose we could countermeasure a problem of damage from parts being dropped by writing an approved work instruction stating "Gravity does not exist in our facility.") This is not the correct approach but in some cases understanding how the effects work can give you the opportunity to cheat the physics that make them occur. For example: If we were re-working a step height on several pieces in our 76°F shop and because of the schedule we needed to inspect them at the machine and not across the shop in the lab, we could set up a gage block stack at the specification nominal (we’ll say 4.2150") and using a 0.0001" dial indicator, set to the gage blocks, we could measure the deviation of each piece to confirm it’s within the (+0.0005", -0.0000") tolerance.

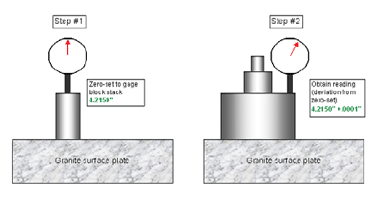Now we have a dilemma. We know the thermal expansion in our 76°F shop on a 4" part causes the part to "grow" 2 tenths, which may lead us to believe our (4.2151") part will measure too small at 68°F. Understanding the simple science and setup of how and when thermal effects occur allows us to rest easy with this application. There is a thermal effect within this application but the expansion is constant between the gage block stack and the part. If the part measures 0.0001" larger than the gage block stack in the 76°F shop environment, then it will also measure 0.0001" larger than the gage block stack when the gage blocks and the part are allowed to stabilize or "soak" to 68°F. This concept holds as long as the gage block stack remained in the 76°F shop environment long enough prior to setup to stabilize to the part temperature.

Thinking about our earlier example using a 0.0001" resolution micrometer; We could obtain separate 1", 2", and 3" gage blocks and have them calibrated annually with our 81 block set. These additional gage blocks can be stored (with care) in the shop to use as controlled micrometer setting masters. Now the zero-setting of our micrometer is thermally stable to our part being measured. It’s just a thought. Even the most detailed concepts of industrial precision measurement break down to counting beads on a string. Thermal effects can be a hot topic, but if you know the math and science of the game, you need not get burned.

Richard Clark is a metrologist who has designed and implemented measurement equipment control systems for several QS-9000 and TS-16949 industrial facilities. To receive more in-depth information about realistic thermal effects (including a freeware version of his Thermal Effects Calculator for Excel) and fast "soaking" times when inspecting your work pieces, e-mail feedback to rcmetrology@yahoo.com.